Беседы о ракетных двигателях

Урок 05. Тепловой расчёт камеры. Способ второй — лирический (ч.1)

Я приветствую Вас, друзья, на очередном уроке по расчёту камер ЖРД.

В прошлом уроке мы с Вами познакомились с программой термодинамического расчёта, которая, конечно же, существенно упрощает жизнь студента, да и инженера тоже. Однако, как я уже отмечал, она не даёт понимания сути расчёта. Мы просто задаём данные и на выходе получаем результат. Для полноценного понимания нужно знать, что происходит внутри программы. Именно этому вопросу я и хочу посвятить несколько следующих уроков.

В данных уроках я не ставлю перед собой цели подробного изложения теории. Для изучения соответствующих разделов отсылаю Вас в Базу знаний или к классическим учебникам. Отмечу лишь, что Вы, как будущий инженер, прежде чем приступать к расчётам, должны иметь представление о том, что такое прямые и обратные химические реакции и что такое динамическое равновесие между ними. Также необходимо помнить, что тепловой расчёт ведётся в предположении о равновесном процессе расширения продуктов сгорания в камере, т.е. о таком процессе, когда состав продуктов сгорания меняется вслед за изменением их термодинамических параметров.

С чего же начинается тепловой расчёт? Здесь логика простая — если мы хотим знать состав продуктов сгорания, то, наверное, нужно знать и какие именно химические реакции протекают в камере ЖРД. Так как топливные компоненты обычно состоят только лишь из углерода, водорода, кислорода и азота, то и количество химических реакций не так велико. Чаще всего ограничиваются рассмотрением 7-8 наиболее весомых реакций.

Далее, если помните, в предыдущих уроках мы говорили, что состав топлива задают массовыми или объёмными долями. Когда же мы имеем дело с газовыми смесями (продуктами сгорания) удобно задавать их состав с помощью парциальных давлений газов.

Всё вышесказанное приводит нас к составлению уравнений констант равновесия основных химических реакций. Ниже записаны такие уравнения. Константы равновесия в них выражены через парциальные давления. Какая константа, какой реакции соответствует, и значения самих констант в зависимости от температуры можно посмотреть в нашем справочном разделе.

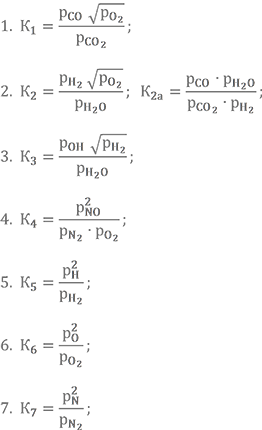
В этих уравнениях переменных заметно больше, чем уравнений. Для замыкания системы добавляют ещё четыре так называемых уравнения баланса элементов, уравнение равенства энтальпии топлива и энтальпии продуктов сгорания при температуре в камере сгорания, уравнение, связывающее суммарную молекулярную массу с парциальными давлениями и уравнение равенства суммы парциальных давлений суммарному давлению газов в камере сгорания (уравнение Дальтона). Вот они.

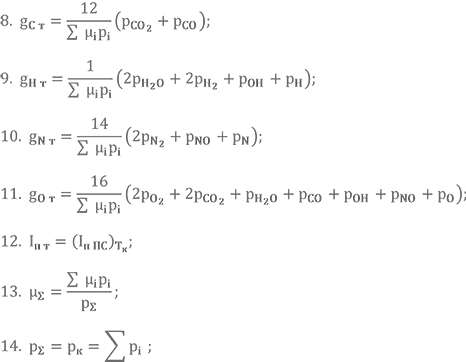
В итоге мы получаем систему из 14 уравнений. И, поверьте, просто так решить её нелегко. Существует несколько методов её решения. Среди наиболее применимых можно выделить метод последовательных приближений и матричный метод.

Акцентирую Ваше внимание на том, что сейчас в практических уроках нас будет интересовать именно решение этой системы, а не её составление. О том, почему в систему входят именно эти уравнения, читайте в соответствующих теоретических материалах.

Также в теории доказывается, что данная система имеет только одно решение, в котором все корни уравнения вещественные и положительные. Именно они нас и интересуют.

Мы рассмотрим решение методом последовательных приближений. Причем решения несколько отличаются в случае использования или неиспользования азотсодержащих компонентов топлива.

И ещё несколько слов о константах равновесия. Константа равновесия химической реакции — это численное выражение определённой пропорции между исходными веществами и продуктами реакции, при которой скорости протекания прямой и обратной реакций равны. Константы они на то и константы, чтобы не меняться. Однако со временем значения этих констант уточняют, и Вы можете найти расхождения между значениями, приведёнными на нашем сайте, и в другой справочной литературе.

Сегодняшний урок я подвожу к концу, чтобы в следующий раз сразу начать изложение методики.

Надолго не прощаюсь. Удачи!