Урок 11. Тепловой расчёт камеры. Способ второй — лирический (ч.7)
С Новым годом, дорогие друзья! С Рождеством Христовым! За новогодними хлопотами дни пролетают совершенно незаметно. Наконец, я выкроил немного времени, чтобы всё-таки закончить наш тепловой расчёт. Да и осталось всего ничего — рассмотреть особенности решения системы для продуктов сгорания, не содержащих азот и получить удельный импульс, имея значения полной энтальпии в камере сгорания и на срезе сопла.
Итак, что у нас получается. В качестве не содержащей азот топливной пары мы использовали керосин + O2(Ж). Смотрим в таблицу топливных пар — для этого топлива значение nиз = 1,146. В других литературных источниках рекомендуют 1,12…1,14. Возьмём nиз = 1,14. Кроме того, для этого варианта мы не вычисляли температуру в камере сгорания. Повторять уже несколько раз использованный нами графический метод я не буду. Думаю, Вы уже сможете, если нужно, сделать всё самостоятельно. Я же воспользовался программой , которая дала мне значение Тк = 3668 К (для ра = 0,008 МПа и αок = 0,8). Посчитаем ожидаемую температуру
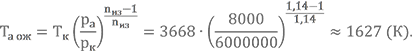
Три температуры в окрестности ожидаемой 1500, 1600, 1700 К. Опять же, решение системы проводим методом последовательных приближений без учёта газов диссоциации и свободного кислорода. Коэффициенты А и Б у нас посчитаны (см. Урок 7): А = 2,34; Б = 1,267.
Далее необходимо задаться значением парциального давления рН2О. Для ориентации воспользуемся таблицей парциальных давлений, из которой выберем отношение рН2О/ра. Для нашего случая точного значения ра нет, выберем рН2О/ра приблизительно — 0,395, тогда рН2О = 3160 Па. Разберём нахождение парциальных давлений для одного значения температуры.
Считаем параметры Y и Ф (К2а = 2,699 для Т = 1500 К, см. таблицу констант равновесия)
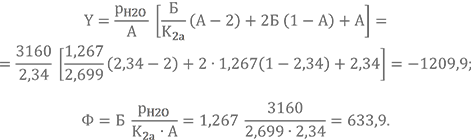
Решаем квадратное уравнение относительно рСО2
т.е. в нашем случае
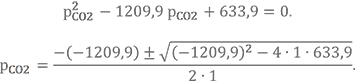
Получаем
Второе значение соответствует практически полному отсутствию СО₂ в продуктах сгорания, что маловероятно, поэтому выбираем первый корень.
Определяем парциальное давление рСО
и рH2
Проверяем по сумме парциальных давлений
Погрешность
Для подобных расчётов это слишком большая погрешность. Необходимо добиться расхождения не более 0,2%. Так как превышение суммы парциальных давлений составило около 5%, давайте новое значение рН2О возьмём на 5% меньше, т.е. ≈ 3000 К. Для облегчения расчётов, как Вы уже догадались, заложим алгоритм в Excel (файл можно взять здесь), а результаты расчётов сведём в таблицу.
| Т, К | p, Па | |||
|---|---|---|---|---|
| pH2O | pCO2 | pCO | pH2 | |
| 1500 | 3007 | 1152 | 1952 | 1889 |
| 1600 | 3119 | 1224 | 2018 | 1639 |
| 1700 | 3202 | 1279 | 2066 | 1454 |
После определения состава продуктов сгорания остаётся найти температуру газов на срезе сопла, а также все остальные параметры газовой смеси. Это мы с Вами уже проделывали на прошлом уроке. Думаю, Вы справитесь.
На этом термодинамический расчёт можно считать законченным (ф-фух!).
Однако если помните, я упоминал о критическом сечении. Тут ничего сложного. Принцип нахождения параметров аналогичен срезу сопла с той лишь разницей, что давление в критическом сечении заранее неизвестно. Найти его можно, вычислив критический перепад давления по формуле
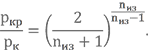
А более точное значение показателя изоэнтропы определить по формуле
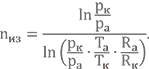
Давайте попробуем посчитать его. Вернёмся к нашему азотсодержащему топливу и вспомним полученные ранее значения и необходимые исходные данные: рк = 6 МПа; ра = 0,008 МПа; Тк = 3405 К; Та = 1215 К; Rк = 0,359 кДж/(кг·К); Rа = 0,343 кДж/(кг·К).
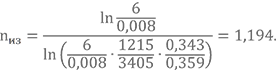
Здесь стоит оговориться, что полученный таким образом показатель изоэнтропы имеет некоторое усреднённое значение. В действительности на участках до критического сечения и после него показатели изоэнтропы расширения продуктов сгорания несколько различаются.
Для будущего расчёта газодинамического профиля нам понадобится ещё такая величина, как расходный комплекс β. Определим её (не забываем подставлять значения в основных единицах измерения, для предыдущей формулы это было не принципиально).
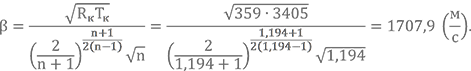
Ну и наконец, давайте выполним завершающее действие — вычислим теоретический удельный импульс нашей камеры. Нам потребуется энтальпия ПС в камере сгорания, равная энтальпии топлива — Iп т = Iп к = 92,5 кДж/кг, и энтальпия ПС на срезе сопла, полученная в Уроке 10 — Iп а = -5100 кДж/кг. Удельный импульс камеры на расчётном режиме равен скорости истечения продуктов сгорания и может быть определён по формуле
Ну что ж, по-моему, вполне правдоподобное значение.
На этом разрешите откланяться. Со следующего урока займёмся ещё одним вариантом определения параметров продуктов сгорания в камере. Вы наверняка уже догадались, что я имею в виду известный справочник «Термодинамических и теплофизических свойств продуктов сгорания» В. П. Глушко.
Удачи всем в Новом году!
| « | Урок 10. Тепловой расчёт камеры. Способ второй — лирический (ч.6) | Урок 12. Тепловой расчёт камеры. Способ третий — альтернативный | » |
