Урок 07. Тепловой расчёт камеры. Способ второй — лирический (ч.3)
 Здравствуйте, друзья!
Здравствуйте, друзья!
Продолжаем изучать тепловой расчёт камеры. Если помните, в прошлый раз мы выяснили, как рассчитать парциальные давления газов в продуктах сгорания, содержащих азот. Тем не менее, нередко бывает, что в исходном топливе азот отсутствует. В этом случае количество уравнений в исходной системе уменьшается, и в умных книжках пишут, что это упрощает её решение. Однако методика в этом случае приводит к необходимости совместного решения двух квадратных уравнений вместо одного, что на упрощение как-то не очень похоже. Кроме того, готовой формулы для нахождения корней системы в книгах обычно тоже не приводится. У Г.Б. Синярёва и М.В. Добровольского предлагается только способ решения с учётом конкретных числовых коэффициентов. Данный факт затрудняет адаптацию алгоритма для последующего ввода в ЭВМ. Поэтому я немного поднатужился 🙂 и вывел итоговую формулу. Ниже Вы сможете её увидеть.
Итак, давайте перейдём ко второму варианту определения парциальных давлений газов в продуктах сгорания при условии отсутствия в них азота.
Для этого случая выберем топливную пару керосин + жидкий кислород. Давление в камере сгорания оставим равным 6 МПа, αок = 0,8. Массовые доли элементов будут равны (см. Уроки 1-3): gCт = 0,234; gHт = 0,036; gOт = 0,730.
Порядок расчёта следующий.
Определяем постоянные А и Б:
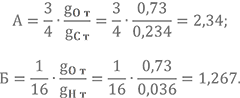
Задаём парциальное давление молекулярного кислорода в первом приближении
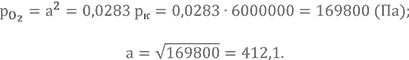
Значение коэффициента перед pк выбираем из таблицы парциальных давлений.
Из таблицы топливных пар выбираем ожидаемое Tк = 3800 К.
Выписываем значения констант равновесия для этой температуры: К1 = 1061; К₂ = 127,9; К3 = 184,0; К5 = 122800; К6 = 108700.
Определяем значения следующих коэффициентов
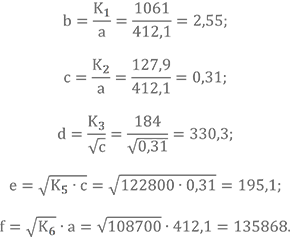
Первое квадратное уравнение записывают следующим образом
![]()
Его можно преобразовать к такому виду
![]()
Второе квадратное уравнение
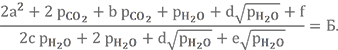
После преобразования оно будет выглядеть так
![]()
Объединяем полученные уравнения в систему
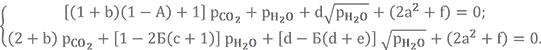
Для упрощения записи обозначим
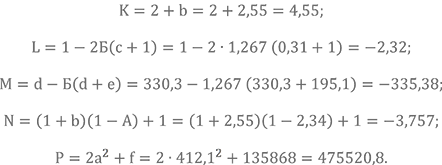
Теперь система выглядит уже не так страшно
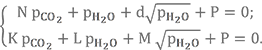
Для исключения одного из неизвестных давлений, например pCO2, умножим второе уравнение системы на N/K и вычтем его из первого. Получим
![]()
Обозначим 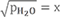 тогда
тогда
![]()
Теперь запишем решение этого квадратного уравнения
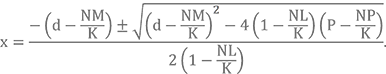
Давайте попытаемся подставить значения коэффициентов
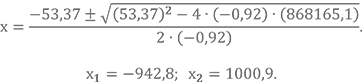
Из двух корней выбираем положительный, что в последствии исключит некорректные значения давлений. В случае выбора отрицательного x, pOH, например, становится отрицательным.
Таким образом, мы определили парциальное давление водяных паров в первом приближении
![]()
Находим парциальные давления остальных газов
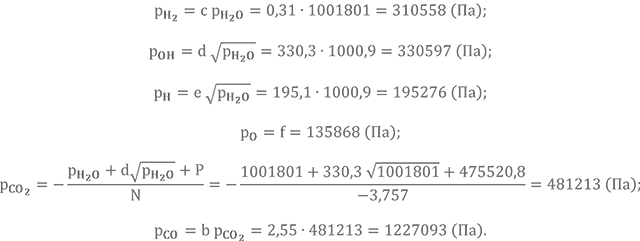
Определяем сумму парциальных давлений
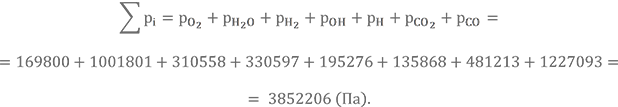
Как видим, сумма существенно отличается от давления в камере сгорания, поэтому необходимо делать следующее приближение, задаваясь новым значением a. Если ∑pi < pк, то выбираем большее значение, если ∑pi > pк, то a уменьшаем. Итерации проводим до обеспечения погрешности на уровне 0,2%.
Как всегда прибегаем к помощи вычислительной техники. Результат расчёта Вы можете увидеть на скриншоте, или скачав данный файл . Здесь проведены расчёты для трёх значений температуры продуктов сгорания в окрестности ожидаемой. Причем в каждой «зоне» расчёта Вы можете видеть два столбца — для первого и некоторого n-го приближений. На самом деле второй столбец приведён для наглядности, чтобы показать, что выдержан необходимый уровень погрешности. Технически же расчёт можно проводить путём подбора вручную коэффициента pO2/pк.
По достижении заданного уровня погрешности рекомендуется выполнить проверку правильности расчёта парциальных давлений с помощью балансных уравнений.
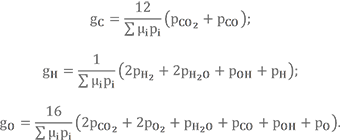
Результаты расчёта для трёх значений температур сводим в таблицу.
| Т, К | p, Па | |||||||
|---|---|---|---|---|---|---|---|---|
| pCO2 | pCO | pH2 | pH2O | pOH | pH | pO2 | pO | |
| 3700 | 968689 | 1832251 | 427672 | 1860409 | 406807 | 187997 | 199200 | 118236 |
| 3800 | 854253 | 1879465 | 455133 | 1716072 | 468041 | 236411 | 232560 | 158995 |
| 3900 | 744358 | 1918133 | 482309 | 1565265 | 526725 | 293497 | 261600 | 207507 |
Что-то многовато на сегодня формул, давайте заканчивать. 🙂
В следующем уроке перейдём к нахождению остальных термодинамических параметров продуктов сгорания.
Всем удачи!
| « | Урок 06. Тепловой расчёт камеры. Способ второй — лирический (ч.2) | Урок 08. Тепловой расчёт камеры. Способ второй — лирический (ч.4) | » |


