Урок 12. Тепловой расчёт камеры. Способ третий — альтернативный
 Здравствуйте, друзья!
Здравствуйте, друзья!
Сегодня я хочу рассказать вам об очень интересном и даже, можно сказать, удобном способе определения параметров продуктов сгорания в камере ЖРД. Я сознательно не говорю о расчёте, потому что называть выбор значений из справочника расчётом как-то не очень правильно. Тем не менее, данный способ позволяет относительно быстро и самое главное, наверно, наиболее точно определить параметры продуктов сгорания практически любой востребованной на практике топливной пары. Для тех из Вас, кто ещё не слышал о так называемом «справочнике Глушко», рекомендую с ним срочно познакомиться. Естественно такую книгу просто так в магазине не купишь. Это многотомное издание сейчас можно встретить наверно только в специализированных библиотеках (да и раньше тоже). Если Вы попытаетесь «погуглить» его в интернете, то, скорее всего кроме 1-го тома ничего не найдёте. Если же найдёте, то поделИтесь ссылкой. Так или иначе, будем считать, что данный справочник попал Вам в руки. Однако, неопытному студенту наверняка потребуется подсказчик, который поможет не утонуть в том море информации и просто табличных данных, которые представлены в справочнике. На сегодняшнем уроке таким подсказчиком для Вас буду я. 🙂
Каждый раз пытаюсь сделать краткое вступление, чтобы не утомлять читателя, а получается как сейчас. В общем, давайте ближе к делу. Прежде чем искать какие-то конкретные данные, я хочу сделать некоторые пояснения к тому, что и в каком виде представлено в справочнике и как это всё правильно из него «достать». Собственно все эти пояснения приведены в самом справочнике, в томе первом. Я же постараюсь расставить некоторые акценты, заострить Ваше внимание на каких-то ключевых моментах.
Обратимся к части третьей первого тома, начинающейся с главы XIII — «Описание таблиц и графиков». Все вступительные слова, думаю, Вы прочтёте сами. Переворачиваем страницу — здесь приведён пример одной таблицы справочника, все страницы в справочнике идентичны. Выберем одну из страниц (стр.341, т. V — здесь указаны параметры продуктов сгорания топливной пары, близкой к рассматриваемой нами ранее НДМГ + АТ) и на её примере разберём, какие же данные здесь указаны (см. рисунки, кликабельно).
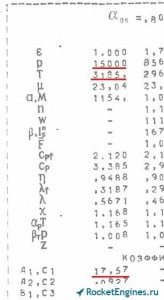
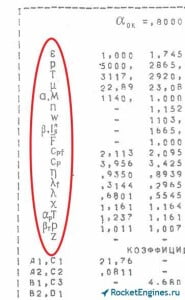
В самом верху страницы записаны несколько параметров, для которых указаны нижеприводимые табличные данные. Это коэффициент избытка окислителя αок, массовое соотношение компонентов топлива k1 (Km), плотность топлива ρт×10-3 в кг/м3 (т.е. чтобы получить значение параметра, значение из таблицы нужно умножить на 103, для нашего рисунка это в частности 1247 кг/м3), полная энтальпия топлива iт (Iп т) в кДж/кг и удельная энтропия s, приведённая к единице массы, в кДж/(кг·К).
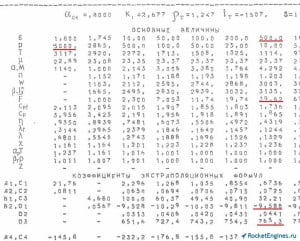
Далее в левом столбце указаны обозначения величин, для которых приводятся числовые данные. В первом числовом столбце приведены значения параметров на входе в сопло (что в предположении о неизменности параметров по длине камеры сгорания соответствует параметрам в самой камере сгорания). Во втором столбце параметры в критическом сечении камеры. В третьем и последующих столбцах — параметры для соответствующей степени расширения. Посмотрим, что за величины указываются в таблице. Первая строка — степень расширения по давлению ε (газодинамическая степень расширения). Первое значение во всех таблицах естественно равно 1, так как расширения ещё нет. Значение из второго числового столбца — критическая степень расширения (критический перепад давлений). Далее фиксированные значения степени расширения.
 |
 |
 |
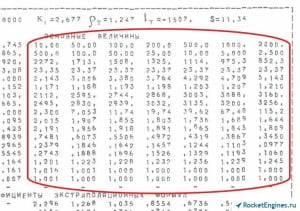 |
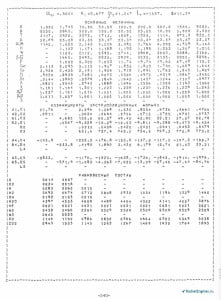
Пройдёмся последовательно по остальным строкам. Вторая строка — давление газовой смеси p в кН/м2, т.е. в кПа. Следующая строка — температура T в К. Далее — молекулярная масса продуктов сгорания μ в кг/моль. В следующей строке обозначены две величины — скорость звука a в м/с и число Маха M. Т.е. в первом столбце приведена скорость звука для условий камеры сгорания, а во втором и последующих число М. Конечно же во втором столбце всегда будет 1. Далее среднее значение показателя изоэнтропы расширения nиз для участка от pс0 (pк) до pс0/ε. В первом столбце прочерк — расширения ещё нет. Идём дальше — скорость газа w в м/с. В первом столбце опять прочерк — поток в камере сгорания считаем неподвижным. Следующая строка — расходный комплекс β в м/с для критической степени расширения (значение приведено во втором числовом столбце), в последующих столбцах — пустотный удельный импульс Isп (Iуд п) в м/с. В следующей строке — геометрическая степень расширения сопла (безразмерная площадь) F = F/Fкр. Во втором столбце опять всё время 1. Остальные величины просто перечислим — это удельная теплоёмкость при постоянном давлении cpf для нереагирующей смеси и cp для реагирующей смеси в кДж/(кг·К); коэффициент динамической вязкости газовой смеси η×107 в (Н·с)/м2 (Па·с) (не путаемся — чтобы получить значение, число из таблицы нужно умножить на 10-7); коэффициент теплопроводности нереагирующей λf и равновесно реагирующей λ смеси в Вт/(м·К); отношение удельных теплоёмкостей при постоянном давлении и постоянном объёме χ = cp/cv (т.е. показатель адиабаты k); произведение изобарного коэффициента расширения на температуру αр×Т; произведение изотермического коэффициента сжатия на давления βт×р; суммарная весовая (массовая) доля веществ в конденсированном состоянии z.
В следующих строках приводятся коэффициенты экстраполяционных формул. Как их использовать поговорим чуть позже. И далее состав продуктов сгорания, выраженный в мольных (объёмных) долях.
Вернёмся к описанию в справочнике. Что представляют собой коэффициенты экстраполяции, и как взаимосвязаны между собой термодинамические величины, почитаете самостоятельно. Мы же перейдём сразу к самому интересному — параграфу 3, в котором с помощью экстраполяционных формул мы можем получить значения величин в произвольных точках.
Давайте рассмотрим их. Первая из них выглядит следующим образом (будем использовать более привычные нам обозначения)
Индексом (0) обозначено значение температуры в камере сгорания в опорной точке. Опорную точку выбираем ближайшую по давлению в камере сгорания (хотя и не обязательно — точность экстраполяции достаточно высокая). ∆ln pк — разность логарифмов давления в КС в опорной точке и в искомой. ∆iт — разность энтальпий топлива в опорной точке и в искомой. Конечно же, энтальпию топлива нужно заранее посчитать (см. Урок 3). Гораздо всё понятнее будет, если рассмотреть пример.
Пример 1
К сожалению тома справочника с топливной парой НДМГ + АТ у меня под рукой не оказалось, поэтому я взял из доступных данных НДМГ + АК-27 (наиболее близкую топливную пару) и те же pк = 6 МПа и αок = 0,8. Определим температуру в камере сгорания. Обращаемся к соответствующему разделу справочника, где приводятся данные для нашей топливной пары. Находим страницы с αок = 0,8 и далее среди давлений (1-й столбец, 2-я строка) выбираем в качестве опорной точки p = 5000 кПа = 5 МПа (см. рисунки внизу). Т.к. αок = 0,8 совпадает с нашим заданным, то третье слагаемое в формуле обнуляется, т.е. разность энтальпий будет равна нулю. Если бы αок отличался от приводимых в справочнике (например, αок = 0,83), для заданного значения необходимо предварительно вычислить энтальпию, чтобы затем определить разность.
Итак, давление в опорной точке 5000 кПа, температура в опорной точке Тк(0) = 3117 К (1-й столбец, 3-я строка). Коэффициент А1 = 21,76 (1-й столбец, строка А1, С1). А₂ нам не понадобится. Подставляем (рекомендуемая точность вычисления логарифмов — до 4-го знака после запятой)
Давайте для сравнения в качестве опорной точки возьмём p = 15000 кПа (следующая страница). Температура в этой опорной точке Тк(0) = 3185 К. Коэффициент А1 = 17,57. Подставим в формулу
Как видим погрешность составляет 4 К или около 0,13%, что говорит об очень высокой точности экстраполяции.
Давайте посмотрим, какие ещё величины мы можем получить. Следующая формула позволяет определить расходный комплекс (удельный импульс давления)
Пример 2
Строительство кирпичного дома на сайте idmdom.ru.
Расходный комплекс в опорной точке (p = 5000 кПа, 8-я строка, 2-й столбец) β = 1665 м/с. Коэффициент B1 = 4,680 (2-й столбец, строка B1, С3). B₂ — не нужен.
Подставляем Как видите, увеличение совсем незначительное.
Переходим к следующей формуле. Пустотный удельный импульс
Обращаю Ваше внимание, что в справочнике имеется опечатка (во всяком случае, в моём экземпляре) — в конце формулы записано ln Δε — это неверно. Будьте внимательны.
Пример 3
Итак, третье слагаемое всё так же обнуляется, но появилось новое — разность логарифмов степени расширения по давлению ε. Степень расширения определяется
как ε = pк/pа. В предыдущих расчётах мы брали pа = 0,008 МПа = 8 кПа. Соответственно ε = 6000/8 = 750. В справочнике приведены степени расширения 500 и 1000. В качестве опорного можно взять любое. Выберем ε = 500. Iуд п в опорной точке — 3135 м/с (8-я строка, столбец с ε = 500), С1 = 0,6736 (строка А1, С1, тот же столбец), С3 = 32,21 (строка B1, С3, тот же столбец). Остаётся подставить всё в формулу
С помощью следующей формулы найдём безразмерную площадь камеры (геометрическую степень расширения сопла)
Пример 4
В опорной точке (ε = 500) F(0) = 39,62; D1 = -9,588; D3 = 765,3; значение D2 не требуется.
Таким образом, мы смогли определить основные термодинамические параметры камеры. Наиболее ценным среди них является удельный импульс, как один из параметров ради которого проводят термодинамический расчёт.
Ниже по тексту в справочнике записаны ещё другие формулы. Они отличаются от только что рассмотренных набором известных исходных параметров. Среди прочих параметров в таблицах приведены значения показателя изоэнтропы, с помощью которого можно определить дополнительные параметры в практически произвольном сечении. Но это уже скорее вопрос теории, и в данном уроке мы его касаться не будем. Также при желании можно использовать интерполяционные формулы, приводимые в следующих подразделах, для получения промежуточных значений величин, неохваченных формулами экстраполяции.
На этом давайте заканчивать — а то экстраполяция, логарифмы — ещё испугаетесь 🙂 . Если что-то покажется непонятным, спрашивайте в комментариях — постараюсь обязательно ответить.
Всем удачи!
| « | Урок 11. Тепловой расчёт камеры. Способ второй — лирический (ч.7) | Урок 13. Определение расхода топлива и основных проходных сечений камеры | » |